Exploring Spectral Graph Theory

In this article, I’ll explore spectral properties of graphs using Linear Algebra. I will make this article as self contained as possible. But, having prior knowledge of Linear Algebra is important. I’ll introduce any background needed.

Set Theory

Mathematics is a language. The definitions of concepts in mathematics are defined precisely. It allows us to reason about them with proofs. The concepts are explained through set theory. Set theory could be used as a possible foundation for mathematics. There is a rigirous treatment of set theory itself called Zermalo-Fraenkel Set Theory. I’ll introduce enough set theory to explain graphs.

Definition: A set is a collection of objects. We could denote the elements of a set in a comma separated list that is enclosed with braces.

Ex:

A = {1, 2, 3, 4}

We could specify an element belongs to a set. The expression 1 \(\varepsilon\) A is read as 1 is a member of A.

Subset

A set can be contained in another set. This relationship is defined by a subset.

Definition: Assume we have two sets A and B. A is a subset of A if every element of A is an element of B. In other words, A is contained in B. This is denoted as A \(\subseteq\) B.

There are two possiblities for subsets. First, A and B could be equal or B could have more elements than A. The case where B has more elements than A is referred to as a proper subset.

Definition: Assume we have two sets A and B and A not equal to B. A is a proper subset of B. B is called the superset of A. This is denoted as A \(\subset\) B.

This diagram shows this relationship among the two sets.

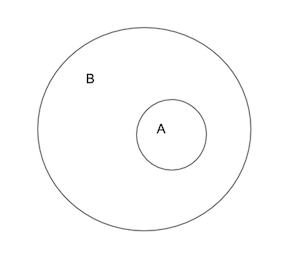
There are basic operations that can be performed on a set. We could take the union and intersection of sets.

Union

Definition: Assume we have two sets A and B. The union of A and B is the set of all elements that are in A or B. This written in set builder notation as \(A \cup B = \{\,x\mid x \in A \lor x \in B\,\}\).

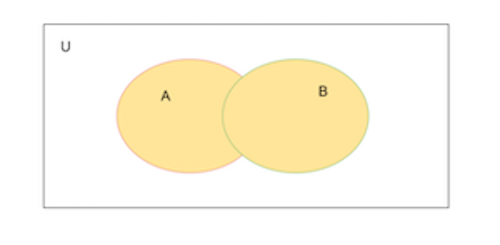
In this diagram, we have a universal set where \(A \subset U\) and \(B \subset U\). The area highlighted above is the set \(A \cup B\).

Intersection

Definition: Assume we have two sets A and B. The intersection of A and B is the set of all elements that are in A and B. This written in set builder notation as \(A \cap B = \{\,x\mid x \in A \land x \in B\,\}\).

Ordered Pairs

Lastly, we’ll define an ordered pair.

Definition: An ordered pair is a pair of objects denoted as (a, b). The ordered pair (a, b) is different from (b, a) unless a == b. On the other hand, an unordered pair is (a, b) does not enforce any ordering.

We could use ordered pairs to define the cartesian product of two sets.

Cartesian Product

Definition: Suppose we have two sets A and B. Their cartesian product is defined as \(A \times B = \{\,(x,y)\mid x \in A \land y \in B \}\) It is the set of all ordered pairs (x, y) such that x is an element of A and y is an element of B.

There are many more topics in set theory. But, this is enough to define a graph and explore their properties.

Graphs

Definition: A graph is an ordered pair G = (V, E). V is the set of all vertices in the graph. E is the set of all edges. \(E \subset \{\,(x,y)\mid x \in V^2 \land x \neq y\}\). \(V^2\) is the set of all vertices that is defined as \(V^2 = V \times V\).

Undirected Graph

As you could from this definition, we are using set theory to define a simple concept of a set. Here is an example of a graph.

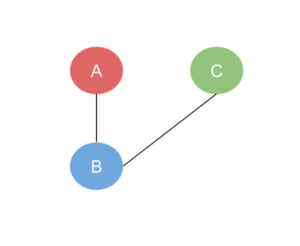
This graph has the vertices V = {A, B, C} and edges E = {(A, B), (B, C)}. This is an example of an undirected graph. There isn’t direction indicated in the connections betweens the vertices. The ordered pairs in the set of edges is unordered.

Directed Graph

Here is an example of a directed graph.

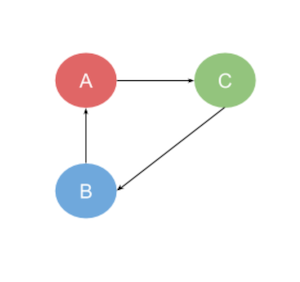
There is directional arrow specified in the edges. This graph has the vertices V = {A, B, C} and the edges E = {(B, A), (A, C), (C, B)}. These are ordered pairs.

Adjaceny Matrix

We could also represent a graph as a matrix, which a rectangular array of numbers. A matrix could defined with various levels of abstraction. Here is a simple definition that suffices for our dicussion.

Definition: A matrix is a rectangular array of numbers. It is enclosed in brackets. A is an m x n matrix with elements at \(a_{mn}\). The subscripts m and n represent the column and row the element is located. Both m and n are positive integers.

A = \(\begin{bmatrix} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ a_{31} & a_{32} & ... & a_{3n}\\ ... & ... & ... & ... \\ a_{m1} & a_{m2} & ... & a_{mn}\\ \end{bmatrix}\)

The representation of a graph is called an adjanceny matrix. Each element of the matrix is indicates whether there is an edge from one vertex to another. This graph’s matrix is the following.

A = \(\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\)

Definition: Assume we have a graph G = (V, E). The values in the adjanceny matrix is described as follows.
\(a_{ij} = \begin{cases} 1 & \text{Edge between vertices}\\ 0 & \text{No edge between vertices}\\ \end{cases}\)

The adjancey matrix allows us to use Linear Algebra to study the spectral properties of the graph.

Symmetry

An interesting feature of an undirected graph’s adjaceny matrix is that it is symmetric. A matrix is symmetrix if it is equal to its transpose.

Definition: Suppose we have an m x n matrix labeled A. The transpose of A is the matrix n x m which is labeled \(A^{T}\).

Example:

A = \(\begin{bmatrix} 1 & 2\\ 3 & 4\\\end{bmatrix}\)

A^T = \(\begin{bmatrix} 1 & 3\\ 2 & 4\\\end{bmatrix}\)

Theorem: The adjaceny matrix for an undirected graph is symmetric. But, this is not true for a directed graph.

This is the adjaceny matrix of the undirect graph we looked at earlier.

A = \(\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\)

Its transpose is the same.

A^T = \(\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\)

Graph Walks

Definition: Suppose we have a graph G = (V, E). A walk from one vertex to another is a sequence of vertices. (v_i, v_j),(v_j, v_k),…, (v_m, v_n) is a walk from a vertex v_i to v_n. The length of the walk is the number of pairs in the sequence.

Example

The sequence (A, B), (B, C) is a walk from A to C.

Theorem: Assume G = (V, E) with adjancey matrix A_G. If we raise A_G to an n-th power, the a_ij element of the matrix gives us the number of walks from v_i and v_j of length n. The value of n is a positive integer.

Example

If we square the adjacency matrix for the undirected graph above, we get the following matrix.

A = \(\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\)

A² = \(\begin{bmatrix} 1 & 0 & 1\\ 0 & 2 & 0\\ 1 & 0 & 1\\ \end{bmatrix}\)

In the matrix A², there is a value of 1 at the location a₀₀. This indicates that there is one walk of length 2 from the vertex A to itself. It is (A, B), (B, A).

The value at location a₁₁ is 2. This means there are 2 walks of length 2 from B to itself. They are (B, C), (C, B) and (B, A) and (A, B).

If we were take powers of A to 3 and higher, we would get a resultant matrix which tells us the number of walk form one vertex to another vertex of length 3 or higher. 


Complete Graph

Definition: A complete graph is a graph each pair of vertices is connected by an edge. It is denoted as M_n where n is the number of vertices.

Example

M₃ =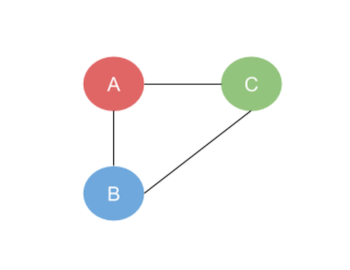

This complete graph has 3 vertices. Its adjacency matrix is the following.

A = \(\begin{bmatrix} 0 & 1 & 1\\ 1 & 0 & 1\\ 1 & 1 & 0\\ \end{bmatrix}\)

The spectrum of this graph M₃ is the eigenvalues of the adjacency matrix and their multiplicities.

Eigenvalues & Eigenvector

Definition: If A is an n x n matrix, then a nonzero vector x in Rⁿ is called an eigenvector of A if Ax = λx for some scalar λ. The scalar λ is called an eigenvalue of A, and x is said to be an eigenvector of A corresponding to λ. ₁

The characteristic equation det(λI – A) = 0, where I is the identity matrix, is used to find the eigenvalues. The left part of the characteristic equation det(λI – A) is called the characteristic polynomial of A.

The characteristic polynomial of M₃(the adjacency matrix of M₃) is the following.

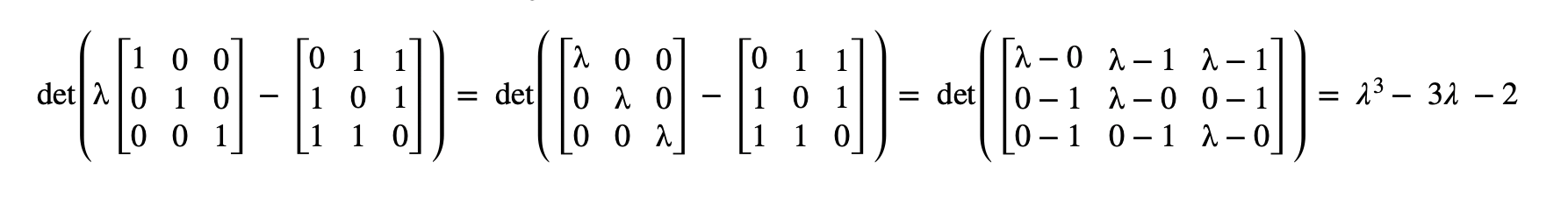
Equating the characteristic polynomial to 0 and finding the roots of the polynomial gives the eigenvalues of A.

λ³ - 3λ - 2 = 0
(λ - 2)(λ + 1)² = 0
(λ - 2)(λ + 1)(λ + 1) = 0

The eigenvalues are λ₀ = -1, λ₁ = -1 and λ₂ = 2. The algebraic multiplicities of the roots are m(λ₀) = 2 and m(λ₂) = 1. The eigenvalues of A and their multiplicities form the spectrum of the complete graph M₃.

Graph spectrum

Definition: The spectrum of a graph is the set of numbers which are eigenvalues of A, together with their multiplicities. If the distinct eigenvalues A are λ₀ > λ₁ > … > λ_s-1, and their multiplicities are m(λ₀), m(λ₁),…,m(λ_s-1), then we shall write.


Spectrum = \(\begin{pmatrix} λ_{0} & λ_{1} & .. & λ_{s-1}\\ m(λ_{0}) & m(λ_{1}) & .. & m(λ_{s-1}) \end{pmatrix}\) ₂

Example:

M₃ =

The spectrum of graph M₃ is the following matrix.

Spectrum M₃ = \(\begin{pmatrix} -1 & 2 \\ 2 & 1 \end{pmatrix}\)

Spectrum Analysis

If we write the characteristic polynomial of M₃ in the form

λⁿ + c₁λ^n-1 + c₂λ^n-2 + c₃λ^n-3 + … + c_n

We could observe information about the sum of the eigenvalues and the trace of the adjacency matrix of M₃.

The characteristic polynomial of M₃ in this form is

λ³ + (-0)λ² + (-3)λ¹ + (-2)

• The coefficient c₁ is 0 which is the sum of the eigenvalues. λ₀ + λ₁ + λ₂ = -1 + -1 + 2 = 0.
• The coefficient c₁ is also the trace of (the adjacency matrix of M₃).

This is true in general for complete graphs. The trace of the adjacency of complete graphs is c1 and sum of the eigenvalues will be the coefficient -c1.

Theorem: The coefficients of the characteristic polynomial of a graph G satisfy the following properties.

1. c1 = 0.
2. –c2 is the number of edges of G.
3. –c3 is twice the number of triangles in G. ₂

Example:

The coefficients of the characteristic polynomial of a graph M₃ satisfy the following.

1. c₁ = 0.
2. –c₂ is the number of edges of G.
3. –c₃ is twice the number of triangles in G.

This theorem is true for complete graphs with at least three vertices. In the characteristic polynomial equation of the adjacency matrix of M₃.

λ³ + (-0)λ² + (-3)λ¹ + (-2)

1. c₁ = 0
   
2. -c₂ = -(-3) = 3 —> The number of edges in the graph M₃.
   
3. –c₃ = -(-2)= 2 —> The number of triangles in M₃ is 1. The coefficient –c₃ = -(-2)= 2 is twice the number of triangles in M₃.
   

Regular graph

Definition: A regular graph is a graph whose vertices all have equal degrees. A m-regular graph is a 

regular graph whose common degree is m.

Example:

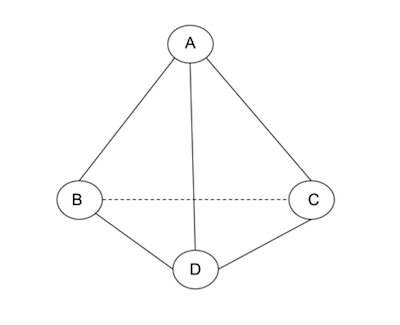
This is an example of a regular of degree 3. Each node has 3 connections in the graph. There are several properties concerning the eigenvalues of regular graphs.

Regular graph spectrum

Definition: If the simple graph G is m-regular, then

(1) m is an eigenvalue of G
(2) the multiplicity of the eigenvalue m is 1, provided G is connected
(3) \(\mid λ \mid \leq m\) for any eigenvalue of G.₂

Example:

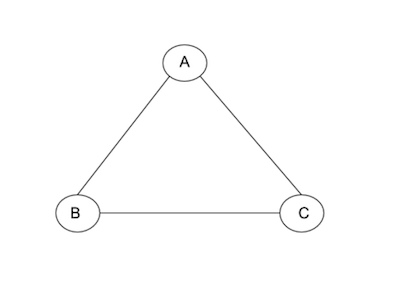
This is an example of a 2-regular graph. Its graph’s adjacency matrix is the following.

A = \(\begin{bmatrix} 0 & 1 & 1\\ 1 & 0 & 1\\ 1 & 1 & 0\\ \end{bmatrix}\)

The characteristic polynomial of this matrix was found to be λ³ - 3λ - 2. The eigenvalues are λ₀ = -1, λ₁ = -1 and λ₂ = 2. The multiplicieties of these eigenvalues are m(λ₀) = 2 and m(λ₂) = 1.

We could observe from the eigenvalues that k (the common degree of the graph) which is 2 is an eigenvalue and its multiplicity is 1. We could also observe that the absolute value of the eigenvalues λ₀, λ₁, λ₂ are less than or equal 2 which is the common degree of the regular graph G. We have confirmed by example properties 1, 2 and 3 hold for a regular graph.

I hope you found this article useful for learning algebraic graph theory.

References

1. Elementar Linear Algebra by Howard Anton

2. Algebraic Graph Theory by Norman Biggs